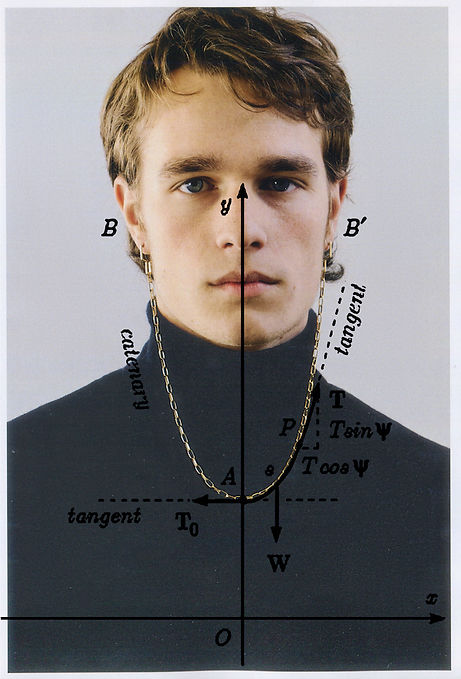
CATENARIA
A catenary is a curve generated by a chain or rope by its own weight, held at both ends and subjected to a uniform gravitational field.
From the Latin catēnarĭus, 'belonging to the chain', the name entitles this collection of chains that hang from one ear to the other as if they were necklaces.
The definition of this curve was the result of mathematically describing the shape that a chain took when it was left hanging, suspended by two points. During the 17th century, many physicists and mathematicians studied the case after seeing that the curve generated by the chains was not a parabola, although it closely resembled one. In fact, until then it had been thought that they were parables. Leibniz, Huygens and Bernoulli derived the equation of the catenary in 1691. In Cartesian coordinates, the equation has this form
where cosh is the hyperbolic cosine function, and where a is the distance of the lowest point above the x axis. All catenary curves are similar to each other, since changing the parameter a is equivalent to a uniform scaling of the curve.
If the two attachment points of the chain are not at the same vertical level, that is, if the catenary that describes the chain is not a symmetrical curve, the shape that will describe the chain will be a segment of the same curve that would be drawn if the ends were at the same height (according to the Cartesian axes, same value for y but different value for x), that is, the same catenary.
Therefore, the chains in this collection always form catenaries because they hang from the ends, wherever they are tied: ear-to-ear, ear-to-nose, ear-to-shirt, ear-to-friend... And they will always be beautiful. Physics is so mundane and so universal that it generates an almost normal beauty, not mediocre but obvious and always the same, as a norm.